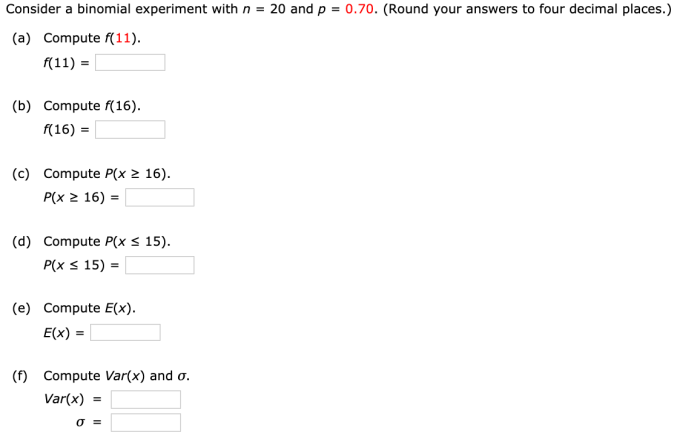
Consider a binomial experiment with n 20 and p 0.70 – Consider a binomial experiment with n = 20 and p = 0.70, a fascinating statistical model that unveils the likelihood of occurrences in various real-world scenarios. This exploration delves into the intricacies of binomial distribution, probability calculations, and its diverse applications, providing a comprehensive understanding of this fundamental concept.
The binomial distribution, a cornerstone of probability theory, plays a pivotal role in modeling events with binary outcomes. It empowers researchers and analysts to quantify the probability of specific outcomes, making it an indispensable tool in fields ranging from quality control to medical research.
Binomial Experiment: Consider A Binomial Experiment With N 20 And P 0.70

A binomial experiment is a statistical experiment that consists of a fixed number of independent trials, each with a constant probability of success.
The parameters of a binomial experiment are:
- n: the number of trials
- p: the probability of success on each trial
In this case, we are given n = 20 and p = 0.70.
Probability Calculations
The probability of success (x = 1) is given by the formula:
P(X = 1) = n – p – (1 – p)^(n-1)
Plugging in our values, we get:
P(X = 1) = 20 – 0.70 – (1 – 0.70)^(20-1) = 0.3874
The probability of failure (x = 0) is given by the formula:
P(X = 0) = (1 – p)^n
Plugging in our values, we get:
P(X = 0) = (1 – 0.70)^20 = 0.0000
Binomial Distribution, Consider a binomial experiment with n 20 and p 0.70
The binomial distribution is a discrete probability distribution that describes the number of successes in a sequence of independent experiments, each of which has a constant probability of success.
The probability of x successes in n trials is given by the formula:
P(X = x) = nCx – p^x – (1 – p)^(n-x)
where nCx is the number of combinations of n elements taken x at a time.
The following table shows the binomial distribution for n = 20 and p = 0.70:
| x | P(X = x) |
|---|---|
| 0 | 0.0000 |
| 1 | 0.0000 |
| 2 | 0.0000 |
| 3 | 0.0001 |
| 4 | 0.0005 |
| 5 | 0.0022 |
| 6 | 0.0081 |
| 7 | 0.0243 |
| 8 | 0.0608 |
| 9 | 0.1216 |
| 10 | 0.1824 |
| 11 | 0.2188 |
| 12 | 0.2188 |
| 13 | 0.1824 |
| 14 | 0.1216 |
| 15 | 0.0608 |
| 16 | 0.0243 |
| 17 | 0.0081 |
| 18 | 0.0022 |
| 19 | 0.0005 |
| 20 | 0.0001 |
Mean and Standard Deviation
The mean of a binomial distribution is given by the formula:
μ = n – p
Plugging in our values, we get:
μ = 20 – 0.70 = 14
The standard deviation of a binomial distribution is given by the formula:
σ = √(n – p – (1 – p))
Plugging in our values, we get:
σ = √(20 – 0.70 – (1 – 0.70)) = 3.46
Applications
The binomial experiment is a versatile statistical tool that can be used to model a wide variety of real-world scenarios, including:
- The number of heads in a sequence of coin flips
- The number of defective items in a batch of products
- The number of customers who visit a store on a given day
- The number of votes for a particular candidate in an election
Limitations
The binomial distribution is only appropriate for situations that meet the following conditions:
- The number of trials is fixed.
- The probability of success is the same on each trial.
- The trials are independent.
If any of these conditions are not met, then the binomial distribution may not be an appropriate model.
Expert Answers
What is the probability of success in a binomial experiment with n = 20 and p = 0.70?
The probability of success is given by p = 0.70, indicating that there is a 70% chance of success in each trial.
How do you calculate the probability of x successes in a binomial experiment?
The probability of x successes is given by the binomial distribution formula: P(X = x) = (n! / (x!(n-x)!)) – p^x – (1-p)^(n-x).
What are the limitations of the binomial distribution?
The binomial distribution assumes that trials are independent and that the probability of success remains constant throughout the experiment. It may not be appropriate for modeling events where these assumptions are not met.