Surface area of prisms and cylinders worksheet answers – Delving into the realm of surface area of prisms and cylinders, this worksheet unravels the intricacies of these geometric shapes, providing a comprehensive guide to their surface area calculations and applications. Embark on a journey of discovery as we explore the formulas, examples, and real-world relevance of surface area in engineering, architecture, and design.
Through a series of engaging explanations, illustrative examples, and meticulously solved problems, this worksheet empowers learners to master the concepts and techniques associated with surface area calculations. By delving into the nuances of prisms and cylinders, we uncover the secrets behind determining their surface areas, equipping students with the knowledge and skills to tackle real-world applications with confidence.
Surface Area of Prisms
Prisms are three-dimensional shapes with two parallel faces called bases and a number of rectangular faces called lateral faces. The surface area of a prism is the sum of the areas of its bases and lateral faces.
Calculating Surface Area of Prisms
The formula for calculating the surface area of a prism is:“`Surface Area = 2(Base Area) + (Lateral Surface Area)“`where:* Base Area is the area of one of the bases
Lateral Surface Area is the sum of the areas of the lateral faces
Examples of Prisms and Their Surface Areas
Here are some examples of different types of prisms and their surface areas:*
-*Rectangular prism
A prism with rectangular bases and rectangular lateral faces. Surface Area = 2(lw + lh + wh)
-
-*Triangular prism
A prism with triangular bases and triangular lateral faces. Surface Area = 2(1/2bh + bl + bh)
-*Pentagonal prism
A prism with pentagonal bases and rectangular lateral faces. Surface Area = 2(1/2ap + as + 5sl)
Table of Surface Areas of Prisms
| Prism Type | Base Area | Lateral Surface Area | Surface Area ||—|—|—|—|| Rectangular prism | lw | 2(lh + wh) | 2(lw + lh + wh) || Triangular prism | 1/2bh | 3bl | 2(1/2bh + bl + bh) || Pentagonal prism | 1/2ap | 5sl | 2(1/2ap + as + 5sl) |
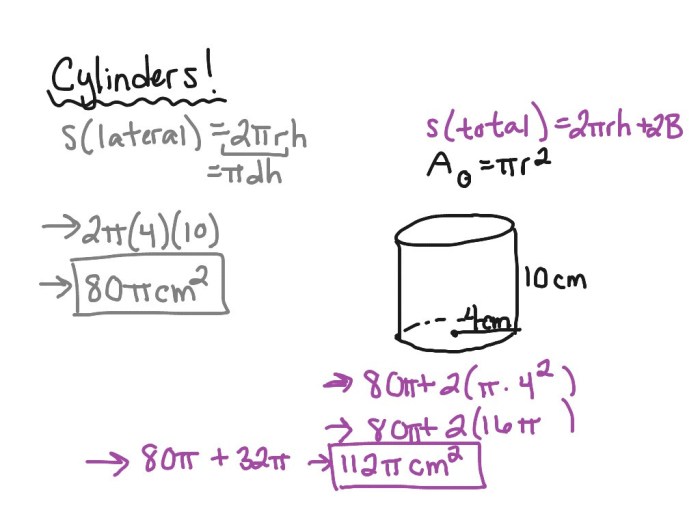
Surface Area of Cylinders: Surface Area Of Prisms And Cylinders Worksheet Answers

Cylinders are three-dimensional shapes with two circular bases and a curved lateral surface. The surface area of a cylinder is the sum of the areas of its bases and lateral surface.
Calculating Surface Area of Cylinders, Surface area of prisms and cylinders worksheet answers
The formula for calculating the surface area of a cylinder is:“`Surface Area = 2(Base Area) + (Lateral Surface Area)“`where:* Base Area is the area of one of the bases
Lateral Surface Area is the area of the curved lateral surface
Examples of Cylinders and Their Surface Areas
Here are some examples of different types of cylinders and their surface areas:*
-*Right circular cylinder
A cylinder with circular bases and a straight lateral surface. Surface Area = 2πr² + 2πrh
-*Oblique circular cylinder
A cylinder with circular bases and a slanted lateral surface. Surface Area = 2πr² + 2πrl
Table of Surface Areas of Cylinders
| Cylinder Type | Base Area | Lateral Surface Area | Surface Area ||—|—|—|—|| Right circular cylinder | πr² | 2πrh | 2πr² + 2πrh || Oblique circular cylinder | πr² | 2πrl | 2πr² + 2πrl |
Helpful Answers
What is the formula for calculating the surface area of a rectangular prism?
Surface Area = 2(lw + lh + wh)
How do I find the surface area of a cylinder?
Surface Area = 2πr(r + h)
What are some real-world applications of surface area?
Surface area is used in engineering to calculate the surface area of buildings, bridges, and other structures. It is also used in architecture to determine the surface area of walls, roofs, and floors. In design, surface area is used to calculate the surface area of products, packaging, and other objects.