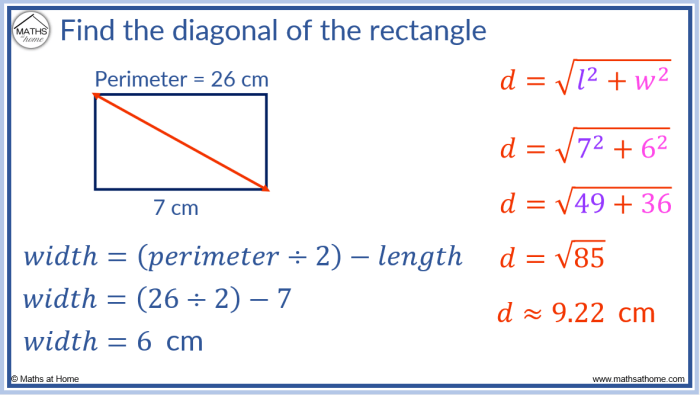
Find the lengths of the diagonals of rectangle $wxyz$ . – Embark on an enlightening journey to determine the lengths of the diagonals in rectangle $wxyz$. This exploration delves into the fundamental properties of rectangles, unlocking the secrets of their diagonal relationships through the lens of the Pythagorean theorem. Prepare to unravel the mathematical intricacies that govern these geometric shapes, gaining a deeper understanding of their applications in diverse fields.

As we delve into the properties of diagonals, we uncover their unique intersection points at the midpoint of each other, establishing a crucial connection between the length, width, and diagonals of a rectangle. This understanding paves the way for the introduction of the Pythagorean theorem, a cornerstone of geometry that empowers us to calculate diagonal lengths with precision.

Rectangle Properties

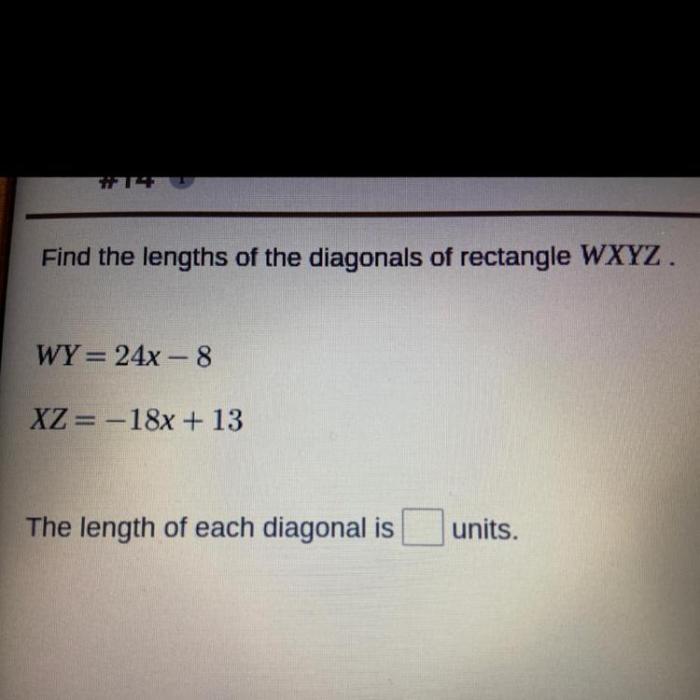
A rectangle is a quadrilateral with four equal angles (90 degrees) and four sides. The two opposite sides are parallel and of equal length. The length and width of a rectangle are the lengths of its two pairs of parallel sides.

Diagonals of a Rectangle

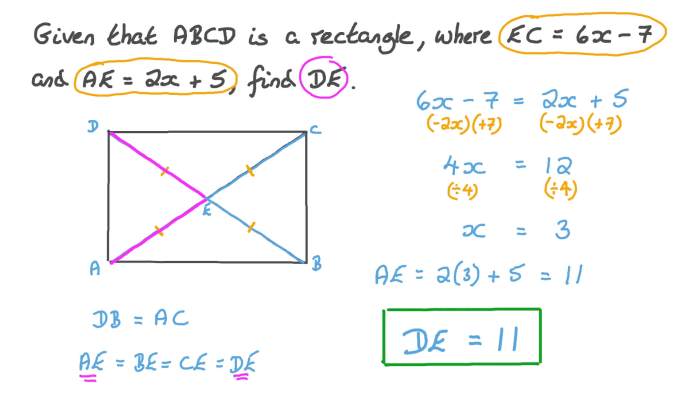
The diagonals of a rectangle are the line segments that connect opposite vertices. They intersect at the midpoint of each other. The diagonals of a rectangle are of equal length.

Relationship between Length, Width, and Diagonals

The relationship between the length (l), width (w), and diagonals (d) of a rectangle is given by the Pythagorean theorem:

d²= l ²+ w ²

Proof of Diagonal Length Formula

To prove the diagonal length formula, we can use the Pythagorean theorem. Let ABCD be a rectangle with length l and width w. Let O be the point of intersection of the diagonals AC and BD.

In right triangle AOB, we have:

AO²+ OB ²= AB ²

In right triangle COD, we have:

CO²+ OD ²= CD ²

Since AO = CO and OB = OD (diagonals intersect at midpoint), we have:

AO²+ OB ²= CO ²+ OD ²

Substituting AB = l and CD = w, we get:

l²+ w ²= 2(AO ²+ OB ²)

Since AC = 2AO and BD = 2OB, we have:

l²+ w ²= 2(AC ²/4 + BD ²/4)

Simplifying, we get:

d²= l ²+ w ²

Applications of Diagonal Length, Find the lengths of the diagonals of rectangle $wxyz$ .

Finding the lengths of diagonals in rectangles has practical applications in various fields, such as:

• Architecture:Determining the diagonal length of a room or building to calculate the maximum length of objects that can fit through doorways or hallways.
• Engineering:Calculating the diagonal length of a rectangular beam or plate to determine its strength and stability.
• Design:Finding the diagonal length of a rectangular canvas or picture frame to ensure that the artwork fits properly.

Frequently Asked Questions: Find The Lengths Of The Diagonals Of Rectangle $wxyz$ .

What is the relationship between the length, width, and diagonals of a rectangle?

The diagonals of a rectangle bisect each other at the midpoint, creating four right triangles. Using the Pythagorean theorem, the diagonal length (d) can be calculated as the square root of the sum of the squares of the length (l) and width (w): d = √(l^2 + w^2).

How can the diagonal length formula be applied in practical situations?

The diagonal length formula finds applications in various fields, including architecture, engineering, and design. For instance, it can be used to determine the length of support beams in a rectangular structure, calculate the diagonal measurements of a room for flooring or tiling purposes, and find the hypotenuse of a right triangle formed by the diagonal and two sides of a rectangle.